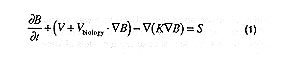
John R. Moisan
Physical Oceanography Research Division
Scripps Institution of Oceanography
University of California, San Diego
La Jolla, CA 92093
January 1995
The Ocean is an extremely complicated system containing many types of physical, chemical and biological processes. Modeling these processes is an arduous task that requires the combined skill of many ocean scientists. Indeed, modeling of the ocean system should be looked upon as a tool for synthesizing those known key processes that play a significant role in the Ocean system as a whole. Over the past decade there has been increased activity in the use of coupled physical-biological models. As an example, the 1994 Woods Hole Program of Summer Study in Geophysical Fluid Dynamics focused on bio-physical models of oceanic population dynamics. With respect to Southern Ocean ecosystem, Michael Sissenwine noted that modeling, "is particularly important for multi-disciplinary, multi-national situations where observations are made and ideas evolve independently. A model is a synthesis of these observations and ideas."
Biological models fall under a wide variety of groups. The discussion for this talk will focus on food web models (Moisan, 1992), size-based models (Moloney and Field, 1991), structured population models (Hofmann and Ambler, 1988) and trophic/generalized food web models (Fasham et al., 1990).
Similar problems arise in all of these models that not only continue to go unresolved but demand much of the time spent in development of a specific model. These problems will prove to be even more difficult and time consuming as we attempt to adapt these models to fully three-dimensional coupled physical-biogeochemical models. Many of these problems have been explicitly outlined in the proceedings of a NATO Advanced Research Workshop entitled, "Towards a Model of Ocean Biogeochemical Processes" (Evans and Fasham, 1993).
Independent of which type of model is chosen, all of the above models typically consist of a set of coupled partial differential equations that govern the space and time distribution of a non-conservative quantity, and are of the form;
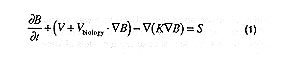
where B is a non-conservative quantity (one of the components in the biogeochemical model); v is the velocity of the fluid, vbiology is the vertical sinking rate and/or behavior of the biological components; K is the kinematic eddy diffusivity (which at a minimum should vary with both time and depth); and, S is the source and sink terms for the biogeochemical processes.
Many such systems of equations are in use today in ecosystem modeling. In developing these types of models, the chief task of the biological modeler is: to determine how many of these equations are needed; to determine how each of the model constituents interact with each of the other constituents (i.e. how are they interconnected by processes such as nutrient uptake, grazing, death and remineralization); to determine how to parameterize this flow of material, such as carbon, nitrogen or some other chemical species; and, finally, to incorporate any behavior processes such as vertical migration or food selection.
The focus of this talk is to see if we can achieve a better, more dynamic, technique for determining how many of these equations are actually needed and what the terms are for S for any given ecosystem. This is currently the key task of the biogeochemical modeler. The impetus for searching for a better technique is due in part to the inability of present day models to adapt to different ecosystems. Indeed, most models must be "reconfigured" for each individual ecosystem modeled. The true test of whether a global biogeochemical model "works" is for it to be able to not only predict the important controlling biological mechanisms [i.e. is the Antarctic iron limited or grazing controlled?], but also predict the productive capacity and food web patterns of that specific ecosystem or biogeographic region. While this of course seems like an impossible task given our current state of model parameter "hardwiring", it is a course of research that offers a new hope in the drive to develop a global biogeochemical model for the Ocean.
To simplify the discussion and comparison of specific model types, all of these component interactions can be placed into a cascade model format (Cohen and Newman, 1985; Newman and Cohen, 1986), an example of which is shown in Table 1. The source/sink term, S, in equation 1 is calculated by summing the column rates of material inflow and subtracting the row of material outflow for each model constituent. As an aside, this technique for calculating S is also a more pragmatic programming technique since it assures conservation of material flow.
| From/To | SiO4 | NO3 | NH4 | DET | LPP | SPP | COP | DOL | EUP |
|---|---|---|---|---|---|---|---|---|---|
| SiO4 | 1 | 1 | |||||||
| NO3 | 1 | 1 | |||||||
| NH4 | 1 | 1 | |||||||
| DET | 1 | 1 | 1 | ||||||
| LPP | 1 | 1 | 1 | 1 | |||||
| SPP | 1 | 1 | |||||||
| COP | 1 | 1 | 1 | ||||||
| DOL | 1 | 1 | |||||||
| EUP | 1 | 1 |
The Cascade Model (CM) was first presented by Newman and Cohen (1986) as a way to analyze the many different types of food webs actually observed in nature. If we restructure all of the known actual ecosystem models (not numerical models, but actual descriptive models of known ecosystems), we begin to see similarities in their structure even as the food webs change in complexity. The first observation that should be strongly noted is that the CM matrix is sparse. While the maximum number of possible interactions,
Present work in this area of food chain research has lead to the development of a dynamic food chain model (Cohen et al., 1990), which examines a hybrid model that combines Lotka-Volterra population dynamics with the Cascade Model's food web structure (LVCM). This more dynamical approach to development of food web models has already been incorporated, although not in a stochastic sense, into a size-based food web model (Armstrong, in press).
The need for incorporating food web dynamics into existing biogeochemical models arises from the need to better simulate the effects that species succession can have on nutrient dynamics and the carbon cycle. The models currently in use today do not allow for such time varying food web structures. However, such time varying food web structures have been observed to occur in nature (Schoenly and Cohen, 1991).
Why not use real measured rates for these interactions? Indeed, field biologists spend incalculable amounts of time collecting such rates. Part of the answer lies in the truth that a measured rate is in fact only the mean value of all the individual rates within a given biological sample from a specific environment.
These measured rates tell us very little about the organism's or population's ability to adapt to changes in their environment. For example, Wood (1992) points out that, "without an estimate of intra-group variation, it is impossible to determine whether or not the differences observed between nominal phytoplankton groups ("species" or otherwise) are any greater than might be observed in a random sample of different members of the same group." In a region like the Antarctic, this point is even stronger due to the paucity of data.
How can these problems be solved? Perhaps we need a more theoretical approach when dealing with biological rates. Are there rules that, like the laws of momentum, allow us to constrain these rates in the biological models? Several biological models have already begun to incorporate these types of rules. As an example, Moisan (1992) incorporated Leibig's "Law of the Minimum" (DeGroot, 1983) into a phytoplankton growth equation that contained three different macronutrients (silicate, nitrate and ammonium). However, these rules are also dependent upon measured variables that again are constrained as constant values in the model.
As an alternative to these types of parameter or even behavior "hardwiring" techniques, Mangel and Clark (1988) present a dynamical approach to modeling biological behavior; and, write that such a modeling approach should follow two hypotheses: "1) That any significant adaptive advantage that is phyletically feasible will tend to be selected; and, 2) Organisms do have some way of getting near to optimal solutions of behavioral problems in situations that they normally encounter." I believe that an optimal dynamic model should allow for such diversity to exist within food web structure, metabolic rates and behavior. The details of this diversity might then help control how each of the members of the food web interacted. As a example, a desirable feature of such a model would be for it to not only allow a silicate-dependent diatom community to dominate wherever the dynamics of the system allow it to; but, also allow other organisms, such as coccolithophores, to flourish within their prospective niches or biogeographic region. If such a more dynamic model was able to simulate present day ocean biogeochemical conditions, it may also be better capable of at least qualitatively simulating (predicting) future changes in the global biogeochemical cycle.
Cohen, J. E. and C. M. Newman, A stochastic theory of community food webs. I. Models and aggregated data, Proc. R. Soc. Lond. B, 224, 153-156, 1985.
Cohen, J. E., T. Luczak, C. M. Newman and Z. -M. Zhou, Stochastic structure and non-linear dynamics of food webs: qualitative stability in a Lotka-Volterra cascade model, Proc. R. Soc. Lond. B., 240, 607-627, 1990.
De Groot, W. T., Modeling the multiple nutrient limitation of algal growth, Ecological Modeling, 18, 99-119, 1983.
Evans, G. T. and M. J. R. Fasham, editors, Towards a Model of Ocean Biogeochemical Processes, NATO ASI Series I: Global Environmental Change, Vol. 10, Springer-Verlag, New York, 350 pages, 1993.
Fasham, M. J. R., Ducklow, H. W. and S. M. McKelvie, A nitrogen-based model of plankton dynamics in the oceanic mixed-layer, J. Mar. Res., 48, 591-639, 1990.
Hofmann, E. E. and J. W. Ambler, Plankton dynamics on the outer southeastern U. S. continental shelf. Part II: A time-dependent biological model, J. Mar. Res., 46, 883-917, 1988.
Mangel, M. and C. W. Clark, Dynamic Modeling in Behavioral Ecology, Princeton University Press, Princeton, NJ, 305 pages, 1988.
Moisan, John R. A Vertical, Time-Dependent Bio-Optical Model. Primary Productivity and Biogeochemical Cycles in the Sea, edited by P. G. Falkowski and A. D. Woodhead, Plenum Press, New York, 522-523, 1992.
Moloney, C. L. and J. G. Field, General allometric equation for rates of nutrient uptake, ingestion, and respiration in plankton organisms, Limnol. Oceanogr., 34, 1290-1299, 1989.
Moloney, C. L. and J. G. Field, The size-based dynamics of plankton food webs, J. Plankton. Res., 13, 1003-1038, 1991.
Newman, C. M. and J. E. Cohen, A stochastic theory of community food webs. IV. Theory of food chain lengths in large food webs, Proc. R. Soc. Lond. B, 228, 355-377, 1986.
Schoenly, K. and J. E. Cohen, Temporal variation in food web structure: 16 empirical cases, Ecol. Monogr., 61, 267-298, 1991.